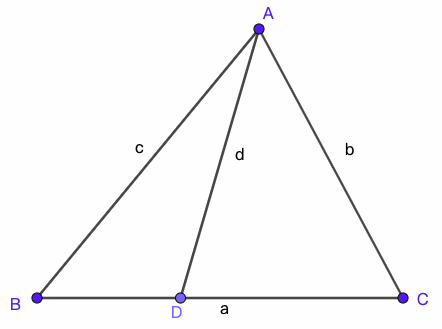
1. 张角定理 张角定理是利用正弦计算三角形面积公式的直接推论.
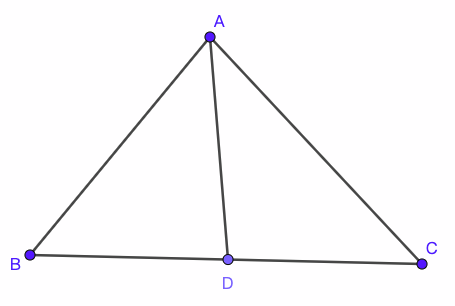
Theorem 1 (张角定理). 如Figure 1, 假设三角形$ABC$中, $BC$边上有一点$D$, 则
\[
\frac{\sin\angle BAD}{AC}+\frac{\sin\angle CAD}{AB}=\frac{\sin\angle BAC}{ AD}.
\]
\[
\frac{\sin\angle BAD}{AC}+\frac{\sin\angle CAD}{AB}=\frac{\sin\angle BAC}{ AD}.
\]
Proof . 利用三角形的面积公式$S_{\triangle ABC}=AB\cdot AC\sin \angle BAC$, 以及$S_{\triangle ABC}=S_{\triangle BAD}+S_{\triangle DAC}$即可.
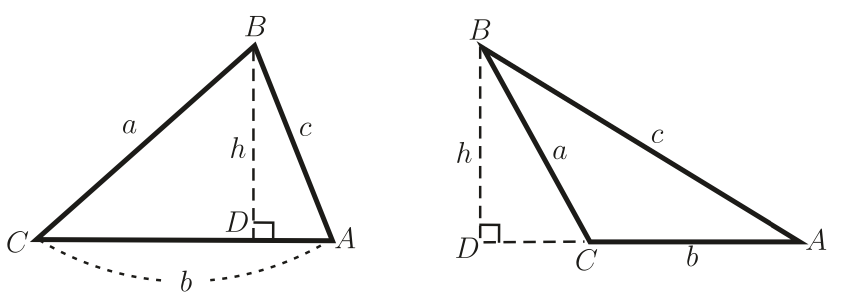
2. 余弦定理 比较有意思的是, 三角形的余弦定理可以直接由勾股定理得到[1].
Theorem 2 (余弦定理). 三角形$ABC$中角$A,B,C$与所对的边长$a,b,c$之间成立
\[
c^2=a^2+b^2-2ab\cos\angle C.
\]
\[
c^2=a^2+b^2-2ab\cos\angle C.
\]
3. 圆的内接四边形余弦定理 关于三角形的余弦定理可以推广到内接四边形[1].
Theorem 3 (圆的内接四边形余弦定理). 圆的内接四边形$ABCD$中角$A,B,C,D$与边长$a=AB,b=BC,c=CD, D=DA$之间成立
\[
a^2+b^2=c^2+d^2-2(ab+cd)\cos\angle D.
\]
\[
a^2+b^2=c^2+d^2-2(ab+cd)\cos\angle D.
\]
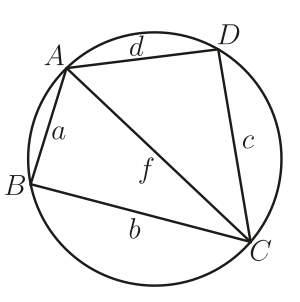
4. 托勒密定理 内接于圆的四边形的各边与对角线之间有下列关系[1].
Theorem 4 (托勒密定理). 假设$ABCD$为圆的内接凸四边形, 则两组对边乘积之和等于对角线的乘积.
Proof . 
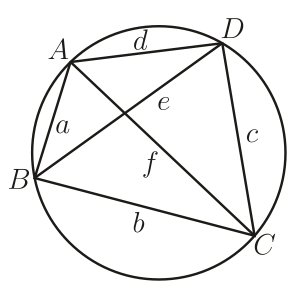
Figure 4. 托勒密定理的证明
如Figure 4所示, 注意到$\angle B+\angle D=\pi$, 利用三角形$ACD$的余弦定理并结合圆的内积四边形的余弦定理, 得到
\begin{align*}
f^2&=c^2+d^2-2cd\cos D\\
&=c^2+d^2-2cd\frac{c^2+d^2-a^2-b^2}{2(ab+cd)}\\
&=\frac{(ad+bc)(ac+bd)}{ab+cd},
\end{align*}
同理, 有
\[
e^2=\frac{(ab+cd)(ac+bd)}{ad+bc},
\]
由此易得结论.
如Figure 4所示, 注意到$\angle B+\angle D=\pi$, 利用三角形$ACD$的余弦定理并结合圆的内积四边形的余弦定理, 得到
\begin{align*}
f^2&=c^2+d^2-2cd\cos D\\
&=c^2+d^2-2cd\frac{c^2+d^2-a^2-b^2}{2(ab+cd)}\\
&=\frac{(ad+bc)(ac+bd)}{ab+cd},
\end{align*}
同理, 有
\[
e^2=\frac{(ab+cd)(ac+bd)}{ad+bc},
\]
由此易得结论.
Remark 1. 由托勒密定理也可证明三角形的余弦定理, 参考[1].
5. 三弦定理 对圆的内接四边形, 我们还有类似张角定理的一个定理.
Theorem 5 (三弦定理). 如Figure 5所示, 假设四边形$ABCD$内接于圆, 则
\[
AB\sin\angle CAD+AC\sin\angle BAD=AD\sin\angle BAC.
\]
\[
AB\sin\angle CAD+AC\sin\angle BAD=AD\sin\angle BAC.
\]
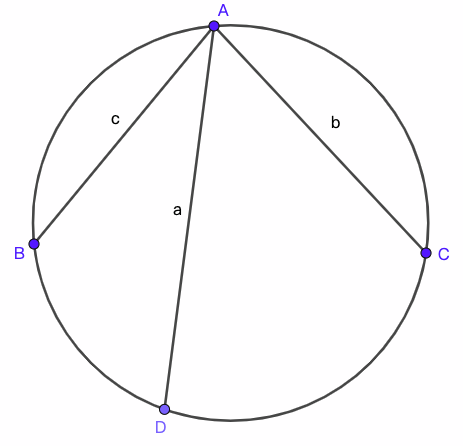
Proof . 令$a=AD$, $b=AC$, $c=AB$, $d=BD$, $e=CD$, $f=BC$. 又令$\angle BAD=\beta$, $\angle CAD=\gamma$则只需证明
\[
a\sin(\beta+\gamma)=b\sin\beta+c\sin\gamma.
\]
利用正弦定理容易得到
\[
2R\sin(\beta+\gamma)=f,\quad
2R\sin\beta=d,\quad
2R\sin\gamma=e.
\]
故只需证明
\[
af=bd+ec,
\]
由托勒密定理知上式成立.
\[
a\sin(\beta+\gamma)=b\sin\beta+c\sin\gamma.
\]
利用正弦定理容易得到
\[
2R\sin(\beta+\gamma)=f,\quad
2R\sin\beta=d,\quad
2R\sin\gamma=e.
\]
故只需证明
\[
af=bd+ec,
\]
由托勒密定理知上式成立.
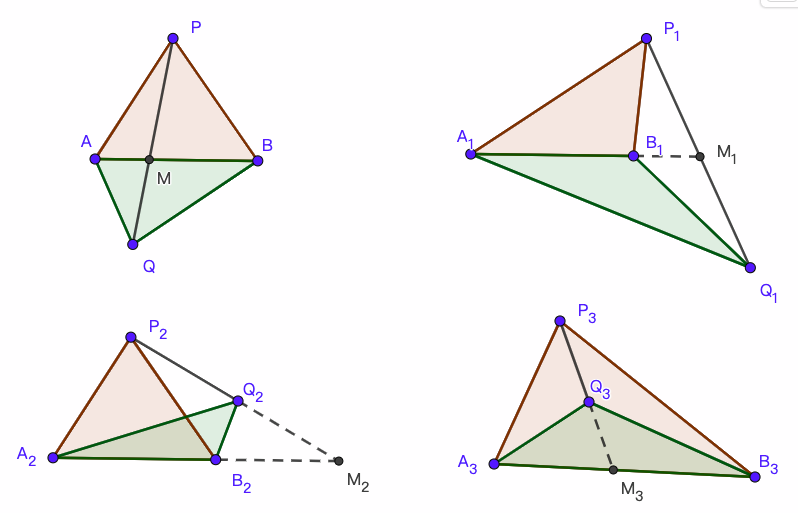
6. 共边定理 共边定理非常简洁, 有着广泛的应用. 在张景中院士的《新概念几何》中用来证明塞瓦定理、梅涅劳斯定理都只用一行.
Theorem 6 (共边定理). 假设三角形$ABP$, $ABQ$具有公共的底边$AB$, 若$PQ$的连线(的延长线)交$AB$(的延长线)于点$M$, 则
\[
\frac{PM}{QM}=\frac{S_{\triangle PAB}}{S_{\triangle QAB}}.
\]
\[
\frac{PM}{QM}=\frac{S_{\triangle PAB}}{S_{\triangle QAB}}.
\]
7. 塞瓦定理 我们称三角形顶点与其对边或对边延长线上一点的相连而成的线段为塞瓦线段.
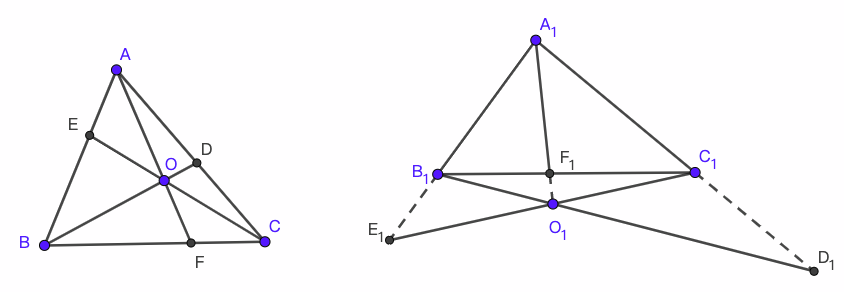
Theorem 7 (塞瓦定理). 三角形$ABC$的塞瓦线段$AF$、$BD$、$CE$, 它们通过同一点$O$的充要条件是
\[
\frac{AE}{EB}\frac{BF}{FC}\frac{CD}{DA}=1.
\]
\[
\frac{AE}{EB}\frac{BF}{FC}\frac{CD}{DA}=1.
\]
Proof . 如Figure 7所示, 利用共边定理我们得到
\[
\frac{AE}{EB}\frac{BF}{FC}\frac{CD}{DA}
=\frac{S_{\triangle OCA}}{S_{\triangle OCB}}
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}
=1.
\]
\[
\frac{AE}{EB}\frac{BF}{FC}\frac{CD}{DA}
=\frac{S_{\triangle OCA}}{S_{\triangle OCB}}
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}
=1.
\]
Corollary 8 (角元塞瓦定理). 假设如塞瓦定理一样. 则
\[
\frac{\sin\angle OAC}{\sin\angle OBC}
\frac{\sin\angle OBA}{\sin\angle OCA}
\frac{\sin\angle OCB}{\sin\angle OAB}=1.
\]
\[
\frac{\sin\angle OAC}{\sin\angle OBC}
\frac{\sin\angle OBA}{\sin\angle OCA}
\frac{\sin\angle OCB}{\sin\angle OAB}=1.
\]
Proof . 只需注意到
\begin{align*}
\frac{S_{\triangle OCA}}{S_{\triangle OCB}}&=\frac{OA\cdot AC\sin\angle OAC}{OB\cdot BC\sin\angle OBC},\\
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}&=\frac{OB\cdot BA\sin\angle OBA}{OC\cdot CA\sin\angle OCA},\\
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}&=\frac{OC\cdot CB\sin\angle OCB}{OA\cdot AB\sin\angle OAB},
\end{align*}
三式相乘得到
\[
1=\frac{S_{\triangle OCA}}{S_{\triangle OCB}}
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}=
\frac{\sin\angle OAC}{\sin\angle OBC}
\frac{\sin\angle OBA}{\sin\angle OCA}
\frac{\sin\angle OCB}{\sin\angle OAB}.
\]
\begin{align*}
\frac{S_{\triangle OCA}}{S_{\triangle OCB}}&=\frac{OA\cdot AC\sin\angle OAC}{OB\cdot BC\sin\angle OBC},\\
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}&=\frac{OB\cdot BA\sin\angle OBA}{OC\cdot CA\sin\angle OCA},\\
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}&=\frac{OC\cdot CB\sin\angle OCB}{OA\cdot AB\sin\angle OAB},
\end{align*}
三式相乘得到
\[
1=\frac{S_{\triangle OCA}}{S_{\triangle OCB}}
\frac{S_{\triangle OAB}}{S_{\triangle OAC}}
\frac{S_{\triangle OBC}}{S_{\triangle OBA}}=
\frac{\sin\angle OAC}{\sin\angle OBC}
\frac{\sin\angle OBA}{\sin\angle OCA}
\frac{\sin\angle OCB}{\sin\angle OAB}.
\]
8. 梅涅劳斯定理 从射影几何的观点来看, 梅涅劳斯定理是塞瓦定理的对偶定理.
Theorem 9 (梅涅劳斯定理). 三角形$ABC$中, 假设点$L, M, N$在边$BC$、$CA$、$AB$或其延长线上, 则$L, M, N$共线的充要条件是
\[
\frac{AN}{NB}\frac{BL}{LC}\frac{CM}{MA}=1.
\]
\[
\frac{AN}{NB}\frac{BL}{LC}\frac{CM}{MA}=1.
\]
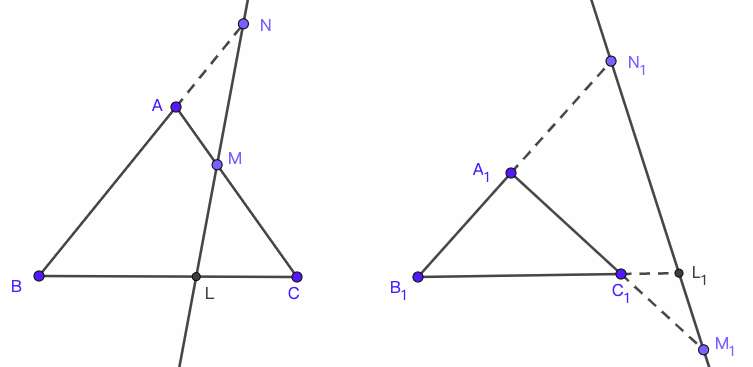
Proof . 如Figure 8所示, 我们利用共边定理得到
\[
\frac{AN}{NB}\frac{BL}{LC}\frac{CM}{MA}
=\frac{S_{\triangle LMA}}{S_{\triangle LMB}}
\frac{S_{\triangle LMB}}{S_{\triangle LMC}}
\frac{S_{\triangle LMC}}{S_{\triangle LMA}}
=1.
\]
\[
\frac{AN}{NB}\frac{BL}{LC}\frac{CM}{MA}
=\frac{S_{\triangle LMA}}{S_{\triangle LMB}}
\frac{S_{\triangle LMB}}{S_{\triangle LMC}}
\frac{S_{\triangle LMC}}{S_{\triangle LMA}}
=1.
\]
Theorem 10 (斯图尔特定理/阿波罗尼奥斯定理). 假设$D$为三角形$ABC$中$BC$边上的一点, 角$A,B,C$对应的边长分别为$a,b,c$, 过顶点$A$的塞瓦线段$AD$长度为$d$. 则
\[
DC c^2+DB b^2=a(d^2+DB\cdot DC).
\]
特别地, 当$D$为中线时, 得到阿波罗尼奥斯定理:
\[
c^2+b^2=2(d^2+BD^2).
\]
\[
DC c^2+DB b^2=a(d^2+DB\cdot DC).
\]
特别地, 当$D$为中线时, 得到阿波罗尼奥斯定理:
\[
c^2+b^2=2(d^2+BD^2).
\]
[1] 蔡聰明。五合一定理。數學傳播季刊, 41(4), 60-68, 2017。 Available from : http://web.math.sinica.edu.tw/math_media/d414/41406.pdf.