复叠空间及其复叠引理、单射群

该读书笔记来自Topology and Groups.
1. 复叠映射的两个例子

Example 1. 假设$S=\mathbb{C}\setminus\left\{ 0 \right\}$, 考察连线映射$p: S\to S$, $p(z)=z^2$. 它是一个$2$重满射, 而且局部上有逆映射.

事实上, 如果我们割掉半直线$B^-:=\left\{ z\in S:\mathrm{Im}(z)=0, \mathrm{Re}(z)<0 \right\}$, 则可定义 \[ q_{\pm}: \mathbb{C}\setminus B^-\to \mathbb{C}\setminus\left\{ 0 \right\}, \] 使得$p(q_{\pm}(z))=z$. 这里, $q_{-}=-q_{+}$. 完全类似地, 我们也可以割掉$B^+:=\left\{ z\in S:\mathrm{Im}(z)=0, \mathrm{Re}(z)>0 \right\}$, 进而得到两个映射
\[
\bar{q}_{\pm}: \mathbb{C}\setminus B^+\to \mathbb{C}\setminus\left\{ 0 \right\},
\]
使得$p(\bar{q}_{\pm}(z))=z$.

下面来看一个无穷重的例子.

Example 2. 令$f: \mathbb{C}\to \mathbb{C}\setminus\left\{ 0 \right\}$, $f(z)=e^{iz}$. 该映射是一个无穷重满射(例如$f^{-1}(1)=\left\{ 2\pi n: n\in \mathbb{Z} \right\}$. 在$\mathbb{C}\perp B^+$或者$\mathbb{C}\setminus B^-$上, 我们有无穷多个局部逆映射: $q_n(z)=2\pi n-i\ln z: \mathbb{C}\setminus B\to \mathbb{C}$, 满足$q_n(1)=2\pi n$, $p(q_n(z))=z$.

Remark 1. 在上述两个例子中, 原像集$\mathbb{C}\setminus\left\{ 0 \right\}$以及$\mathbb{C}$可以是非单连通的, 也可以是单连通的. 但是逆映射的原像集$\mathbb{C}\setminus B^{\pm}$都是单连通的.

2. 复叠映射与复叠空间

Definition 1. 假设$p:Y\to X$是一个连续映射.

子集$U\subset X$称为一个基础邻域(elementary neighbourhood), 如果存在离散集$F$, 以及同胚映射(homeomorphism)$h:p^{-1}(U)\to U\times F$, 使得$\mathrm{p}_1\circ h=p|_{p^{-1}(U)}$, 其中$p_1:U\times F\to U$是到第一个因子的投射;
我们称$p$为一个覆盖映射(covering map), 如果$X$被一些基础邻域覆盖, 即对任意的$x\in X$, 都存在一个基础邻域$U$, 使得$x\in U$; 此时, 称$Y$为$X$的一个复叠空间(covering space);
我们称$V\subset Y$为一个基础切片(elementary sheet), 如果$V$是道路连通的而且$p(V)$是一个基础邻域.

Remark 2. 事实上, 复叠空间$Y$也可视为纤维丛$p:Y\to X$, 使得纤维为离散集合$F$. 同胚映射$h:p^{-1}(U)\to U\times F$给出了其局部平凡化.

一般地, $p_n(z)=z^n$将给出一条绕$n$圈的螺旋线. 下图给出了$n=3$的情形:

3. 单射群与道路提升引理

Example 3. 考察单位圆周上的三重复叠映射: $p(e^{i\theta})=e^{3i\theta}$, 每个$s\in S^1$都有$p^{-1}(s)$为三个点. 假设$p^{-1}(1)=\left\{ a,b,c \right\}$, 考察沿着$S^1$上从$1\in S^1$出发的环路(loop), 我们看到原像集从$a$移动到$b$, 然后$b$移动到$c$, 最后$c$移动到$a$. 因此当我们重复环路时, 我们在循环置换$(abc)\in S_3$, 即得到群同态$\pi_1(S^1,1)\to \mathrm{Perm}(p^{-1}(1))=\mathrm{Perm}(a,b,c)=S_3$, 将环路映射到$(abc)$. 由于$(abc)\in S_3$不是平凡的(非恒等置换), 因此环路在$\pi_1(S^1,1)$中也不是平凡的.

更一般地, 单射群是$\pi_1(X,x)$在$p^{-1}(x)$上一个作用, 即群同态$\pi_1(X,x)\to \mathrm{Perm}(p^{-1}(x))$. 这给出了一个确定基本群$\pi_1(X,x)$中非平凡环路的方法. 此外, 存在一个复叠空间(称为万有复叠空间), 使得$\pi_1$中所有元素的作用都是非平凡的.

在上述例子中, 我们没有说清楚什么叫做沿着环路, 原像集从$a$移动到$b$, 这将用道路提升引理(path-lifting lemma)来严格化; 也没说清楚单射群的定义中为什么只依赖于环路的同伦类, 这将用同伦提升引理(homotopy-lifting lemma)来说明.

Theorem 2 (道路提升引理). 假设$p:Y\to X$是一个复叠映射, $\delta:[0,1]\to X$是一条道路, $\delta(0)=x$, 并令$y\in p^{-1}(x)$. 则存在唯一的道路$\gamma:[0,1]\to Y$, 满足$p\circ\gamma=\delta$以及$\gamma(0)=y$. 我们称$\gamma$是$\delta$的一个提升.

Proof . 假设$\mathcal{U}$是映射$p$下$X$的一个由基础邻域构成的开覆盖的集合. 则$\left\{ \delta^{-1}(U): U\in \mathcal{U} \right\}$是$[0,1]$的一个开覆盖, 因此有有限子覆盖. 从而存在有限分割$0=t_0\leq t_1\leq \cdots t_n=1$, 使得$\delta_k:=\delta|_{t_k,t_{k+1}}\subset U_k$, 对某个$U_k\subset \mathcal{U}$.

我们将利用对$k$的归纳法构造$\gamma$.

对$k=0$: 由于要求$\gamma(0)=y$. 注意到$p$是一个覆盖映射, 因此存在局部逆映射$q_0:U_0\to Y$ 使得$q_0(x)=y$, $p\circ q_0=\mathrm{id}|_{U_0}$, 则$\gamma=q_0\circ \delta_0$满足要求: $\gamma(0)=q_0(\delta_0(0))=q_0(x)=y$; $p\circ \gamma=p\circ q_0\circ \delta_0=\mathrm{id}|_{U_0}\circ \delta_0=\delta$.

现在假设我们构造了$\gamma_0,\ldots,\gamma_{k-1}$, 下面来构造$\gamma_k:[t_k,t_{k+1}]\to Y$. 为了使得$\gamma$连续, 我们要求$\gamma_k(t_k)=\gamma_{k-1}(t_k)$. 注意到存在$q_k:U_k\to Y$, 使得$q_k(\delta(t_k))=\gamma_{k-1}(t_k)$, 而且$p\circ q_k=\mathrm{id}|_{U_k}$. 因此, 我们可以定义$\gamma_k=q_k\circ \delta_k$. 由此我们将$\delta$的道路提升映射$\gamma$连续延拓到$[t_k,t_{k+1}]$.

现在, 我们对$t\in[t_k,t_{k+1}]$, 定义$\gamma(t)=\gamma_k(t)$. 则$\gamma$连续, 因为在每个分段定义的函数的重合端点处是连续的. 而且由于在$[t_k,t_{k+1}$上$p\circ \gamma=p\circ q_k\circ\delta_k=\mathrm{id}|_{U_k}\circ\delta_k=\delta_k$, 故$\gamma$还是$\delta$的一个提升.

为了证明唯一性, 我们给出如下更一般的引理:

Lemma 3. 假设$p:Y\to X$是一个覆盖空间. 令$T$是一个连通空间, $F:T\to X$是一个连续映射. 则两个提升映射$\tilde{F}_1,\tilde{F}_2:T\to Y$相等, 即对任意的$t\in T$, 都有$\tilde{F}_1(t)=\tilde{F}_2(T)$, 当且仅当存在一个$t_0\in T$, 使得$\tilde{F}_1(t_0)=\tilde{F}_2(t_0)$.

回忆, $\tilde{F}$称为$F$的一个提升, 如果$p\circ\tilde{F}=F$.

Proof (引理的证明). 令$S=\left\{ t\in T: \tilde{F}_1(t)=\tilde{F}_2(t) \right\}$. 我们希望证明$S$既开又闭. 由于$T$连通, 故这表明$S=\emptyset$或者$S=T$, 但$t_0\in S$, 因此$S=T$.

考察$t\in T$, 令$x=F(t)$. 由于$p:Y\to X$是一个复叠空间, 因此存在基础邻域$x\in W\subset X$以及基础切片$V_1,V_2$, 使得$p(V_1)=W=p(V_2)$, 而且$\tilde{F}_1(t)\in V_1$, $\tilde{F}_2(t)\in V_2$.

由于$\tilde{F}_1$, $\tilde{F}_2$是连续的, 故存在开集$U_1,U_2\in T$使得$t\in U_i$, $\tilde{F}_i(U_i)\subset V_i$, $i=1,2$. 令$U=U_1\cap U_2$.

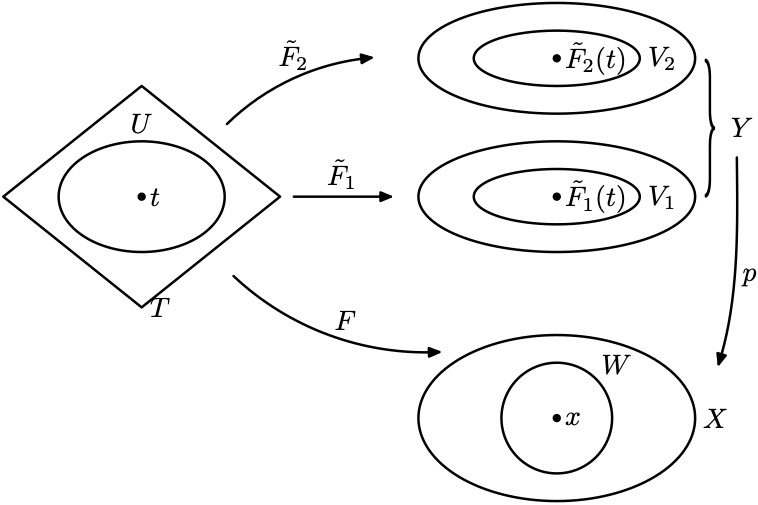
我们希望证明$T\setminus S$为开集. 事实上, 假设$t\in T\setminus S$, 则我们将证明$U\subset T\setminus S$. 这是因为, $t\in T\setminus S$, 故$\tilde{F}_1(t)\neq \tilde{F}_2(t)$, 从而$V_1\cap V_2=\emptyset$. 故对所有的$t’\in U$, 我们都有$\tilde{F}_1(t’)\neq \tilde{F}_2(t’)$(这是因为$t’\in U\implies \tilde{F}_1(t’)\in V_1,\tilde{F}_2(t’)\in V_2$, 而$V_1\cap V_2=\emptyset$).

我们还需要证明$S$为开集. 事实上, 假设$t\in S$, 则$\tilde{F}_1(t)=\tilde{F}_2(t)$, 因此$V_1=V_2=:V$. 由于存在$p$的局部逆映射$q:W\to V$, 即$p\circ q=\mathrm{id}_W$, $q\circ p=\mathrm{id}_V$, 我们知道如果$t’\in U$, 则$\tilde{F}_1(t’)\in V$, $\tilde{F}_2(t’)\in V$, 从而$q(F(t’))=q(p(\tilde{F}_1(t’)))=\tilde{F}_1(t’)$, 类似地$q(F(t’))=\tilde{F}_2(t’)$, 因此$\tilde{F}_1(t’)=\tilde{F}_2(t’)$, 即$U\subset S$.

4. 单射群在前面我们证明了复叠空间中的道路提升引理, 即: 对任意的一个复叠空间$p:X\to Y$, 以及其中任意一条道路$\gamma:[0, I]\to X$, 若$y\in p^{-1}(\gamma(0))$, 则存在道路$\gamma$唯一的提升$\tilde{\gamma}\in Y$, 使得$p\circ \tilde{\gamma}=\gamma$以及$\tilde{\gamma}(0)=y$.

问题是: 如果我们假设$\gamma$是一个环路(loop), 则一般而言, 我们不能保证$\tilde{\gamma}$也是一个环路. 例如, $p:S^1\to S^1$, $p(e^{i\theta})=e^{2i\theta}$, 是二重复叠映射, 则$\tilde\gamma(t)=e^{it\pi}$就是环路$e^{2\pi it}$, $t\in[0,1]$, 的提升. 这就引出单射群的概念.

Definition 4. 假设$p:Y\to X$为一个复叠空间, $\gamma:[0, 1]\to X$是一个以$x$点为基点的环路, 即$\gamma(0)=x=\gamma(1)$. 我们将绕着$\gamma$的单射群定义为置换$\sigma_\gamma:p^{-1}(x)\to p^{-1}(x)$, $\sigma_\gamma(y)=\tilde{\gamma}(1)$, 其中$\tilde{\gamma}$为从$y\in p^{-1}(x)$出发的$\gamma$的提升.

一个基本事实是, 单射群与同伦道路的选择无关, 即

Lemma 5. 假设$p:Y\to X$为复叠空间, 若$\gamma_1\sim\gamma_2$是以$x\in X$为基点的两个同伦环路, 则单射群$\sigma_{\gamma_1}=\sigma_{\gamma_2}$.

为了证明该引理, 我们证明如下更加一般的同伦提升引理.

Lemma 6 (同伦提升引理). 假设$p:Y\to X$是一个复叠空间, $\gamma_s$是$X$中固定端点的同伦道路, 即$\gamma_s(0),\gamma_{s}(1)$都是$X$中与$s$无关的点. 则, 对给定的$\gamma_0$的提升$\tilde{\gamma}_0$, 存在固定端点的同伦提升$\tilde{\gamma}_s$, 即$\tilde{\gamma}_s$是$\tilde{\gamma}_0$的一个同伦, 使得
\[
p\circ\tilde{\gamma}_s=\gamma_s,
\]
而且$\tilde{\gamma}_s(0),\tilde{\gamma}_s(1)$都与$s$无关.

Proof . 假设$H:[0,1]\times[0,1]\to X$是$X$里的一个同伦, 即$\gamma_s(t)=H(s,t)$. 我们可以将$[0,1]\times[0,1]$分成很多小矩形$R_{ij}$, 使得$H(R_{ij})\subset U_{ij}$, 这里$U_{ij}$为$X$的某个基础邻域. 这里, $i, j$指标分别表示$x,y$方向的指标.

我们需要具体构造一个同伦提升$\tilde{H}$, 使得$\tilde{H}(s,t)=\tilde{\gamma}_s(t)$, 自然地, 我们可以利用$p$的局部逆映射$q_{ij}:U_{ij}\to Y$, 构造$\tilde{H}_{R_{ij}}=q_{ij}\circ H|_{R_{ij}}$. 一方面, 这确实是$H$的一个提升, 即$p\circ \tilde{H}=p\circ q_{ij}\circ H=H$在每个$R_{ij}$都成立, 但另一方面, 我们需要恰当的选取$q_{ij}$, 使得如上构造的$\tilde{H}$是连续的, 这本质上要求$\tilde{H}|_{R_{ij}}=\tilde{H}_{R_{kl}}$在$R_{ij}\cap R_{kl}$上成立.

为了简单起见, 假设我们得到一个$2\times 2$的网格. 首先来构造$q_{1j}$. 注意到, $\tilde{H}(0,t)=\tilde{\gamma}_0(t)$, 这里$\tilde{\gamma}_0$是$\gamma_0$的一个提升(固定). 这表明$q_{1j}$应该如何定义, 即$q_{11}:U_{11}\to Y$是$p$局部唯一的逆映射使得$q_{11}(\gamma_0(0))=\tilde{\gamma}_0(0)$, $q_{12}:U_{12}\to Y$是$p$局部唯一的逆映射使得$q_{12}(\gamma_0(t_1))=\tilde{\gamma}_0(t_1)$, 这里$t_1$是$R_{11}$最上面的$t$坐标(在$2\times 2$的情形有$t_1=1$).

我们需要验证$\tilde{H}_{11}:=q_{11}\circ H$, $\tilde{H}_{12}:=q_{12}\circ H$在$R_{11}\cap R_{12}$上是相同的(这个交集其实就是边$\left\{ (s,t_1):s\in[0,s_1] \right\}$). 事实上, 按照构造
\[
\tilde{H}_{11}(0,t_1)=\tilde{H}_{12}(0,t_1)=\tilde{\gamma}_0(t_1),
\]
因此$\tilde{H}_{1j}(s,t_1)$现在到边$R_{11}\cap R_{12}$上定义了两条路径, 他们都是$H(s,t_1)$的提升(因为$p\circ \tilde{H}_{1j}(s,t_1)|_{[0,s_1]}=p\circ q_{1j}\circ H(s,t_1)|_{[0,s_1]}=H(s,t_1)|_{[0,s_1]}$), 而且有相同的初始条件$\tilde{H}_{11}(0,t_1)=\tilde{H}_{12}(0,t_1)=\tilde{\gamma}_0(t_1)$, 因此由道路提升的唯一性, 我们知道$\tilde{H}_{11}(s,t_1)=\tilde{H}_{12}(s,t_1)$对任意的$s\in[0,s_1]$都成立.

利用同样的技巧, 我们从$\tilde{\gamma}_{s_1}$出发, 可以延拓上述同伦到$R_{2j}$, 进而由归纳法, 我们得到整个正方形上的同伦.

我们还需要验证$\tilde{H}$具有固定的端点, 事实上$\tilde{H}(s,0)$是$H(s,0)$的提升是一个常值. 这是因为, 常值提升也是满足条件的一个提升, 因此利用提升的唯一性得到$\tilde{H}(s,0)$必定就是常值提升. 同样的道理可以说吗$\tilde{H}(s,1)$也是常值.

Leave a Reply Cancel reply