极小曲面的分枝点定义为曲面在这样的点处不能用一对一的方式参数化. 从而在分枝点, 曲面并不是通常定义下的几何曲面, 因为通常我们要求在任意一点的邻域内, 看起来像一个完全的圆盘.
带有分枝点的极小曲面是在研究极小曲面的理论时必须考虑的对象, 因为一列没有分枝点的曲面的极限很可能有分枝点, 而这种极小化序列的方法是寻求极小曲面的基本方法之一. 事实上, 关于分枝点的出现, 可以用数学公式完全刻画. 因此我们可以作带有分枝点的曲面的图, 而且保证任何分枝点看起来都和这些图形之一相同.
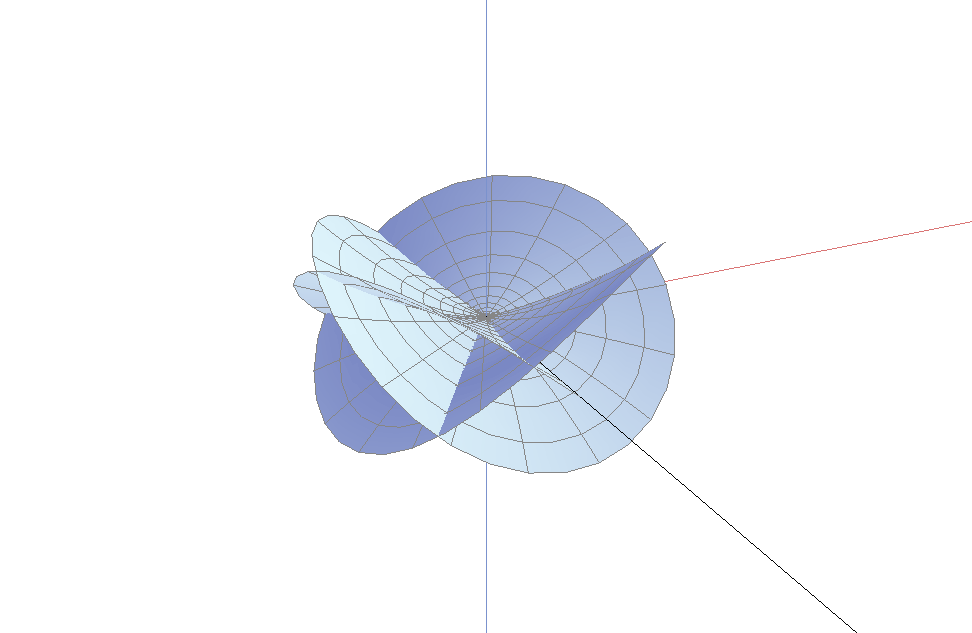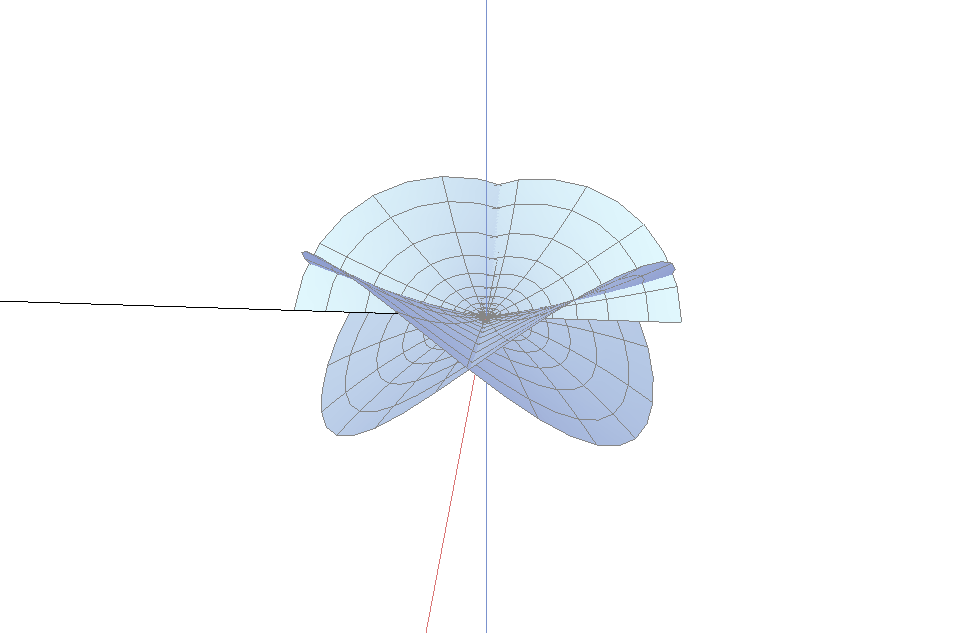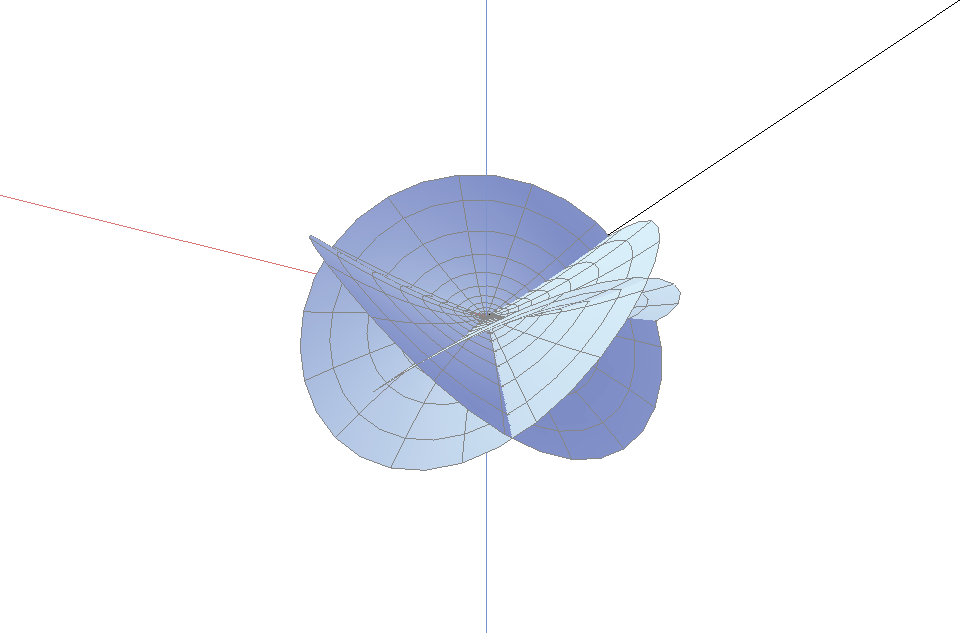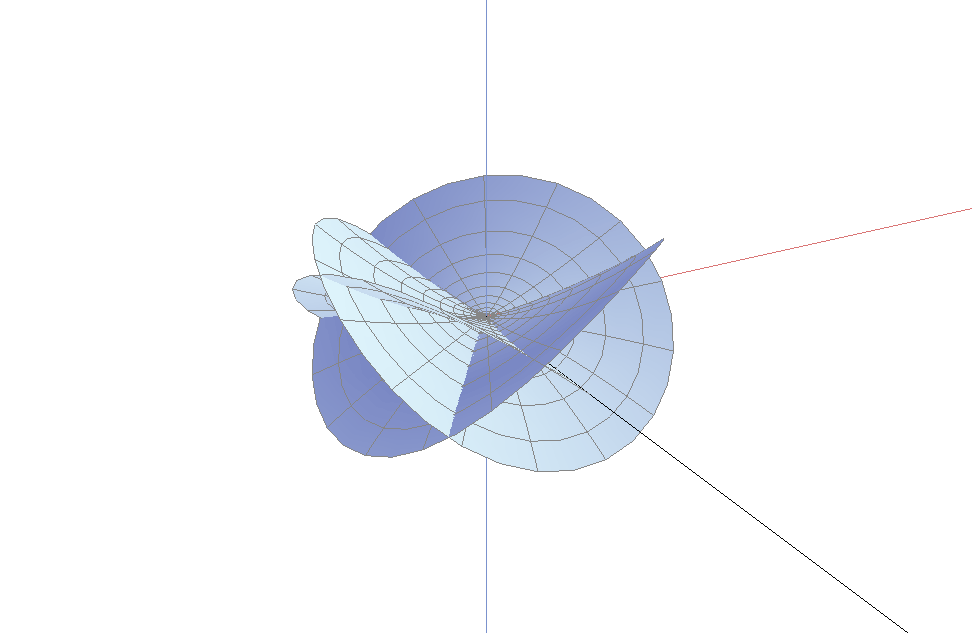
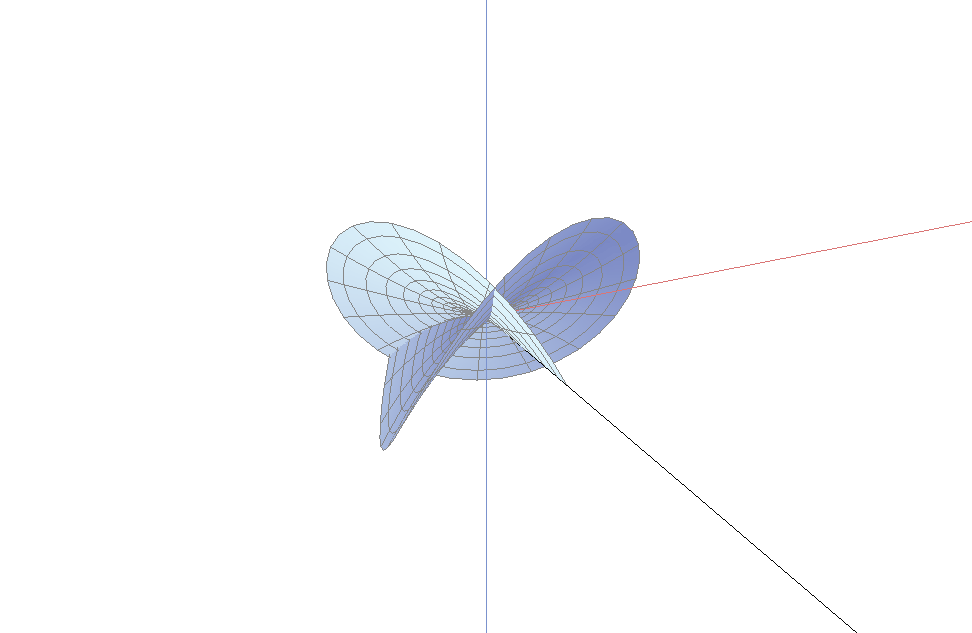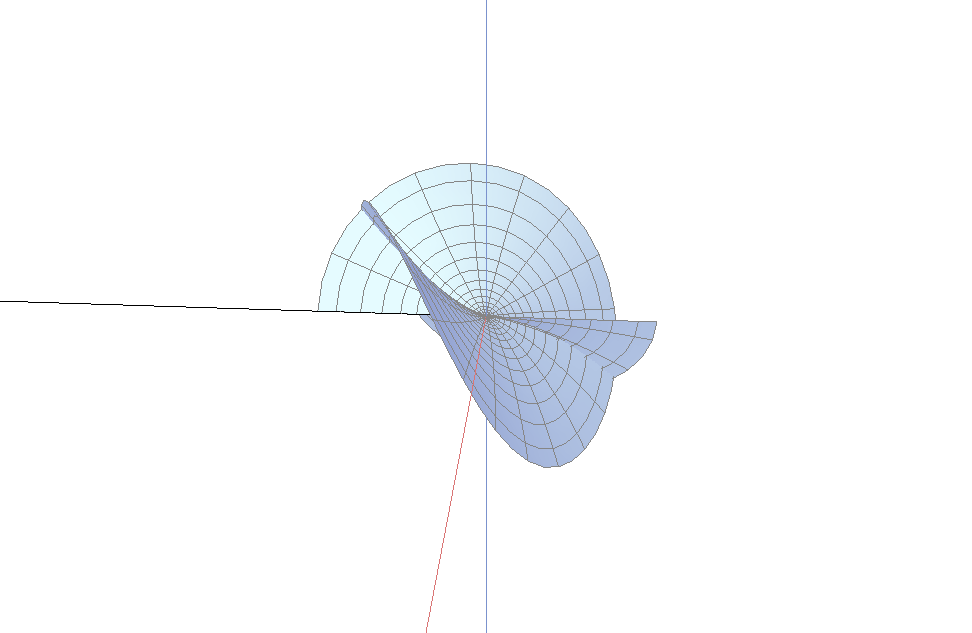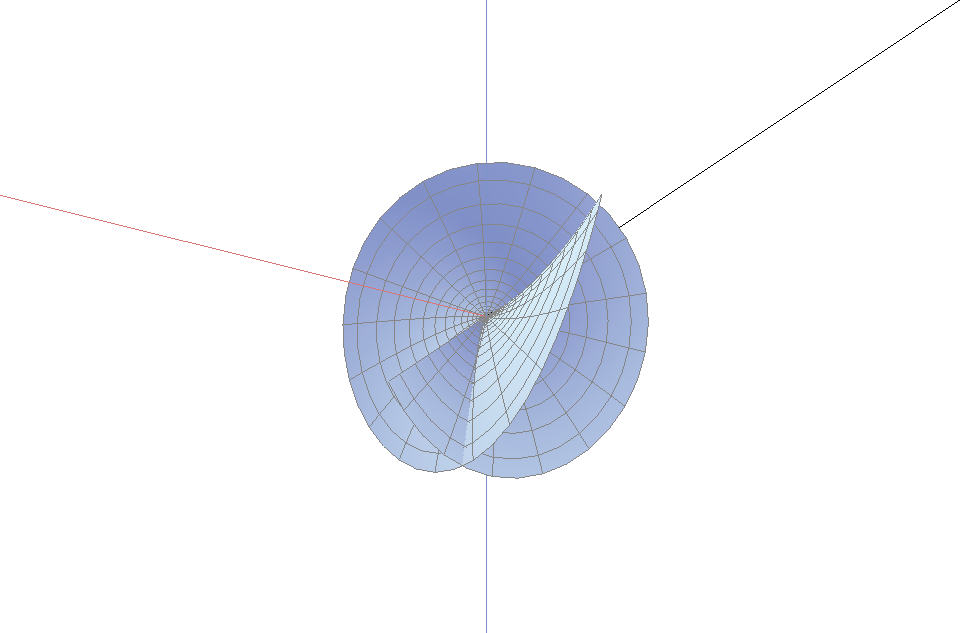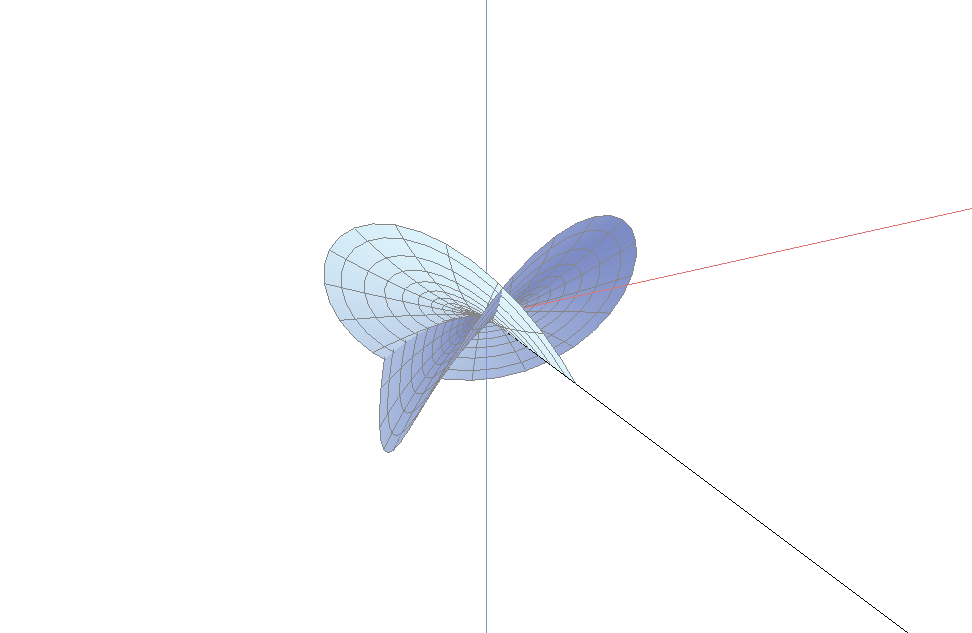
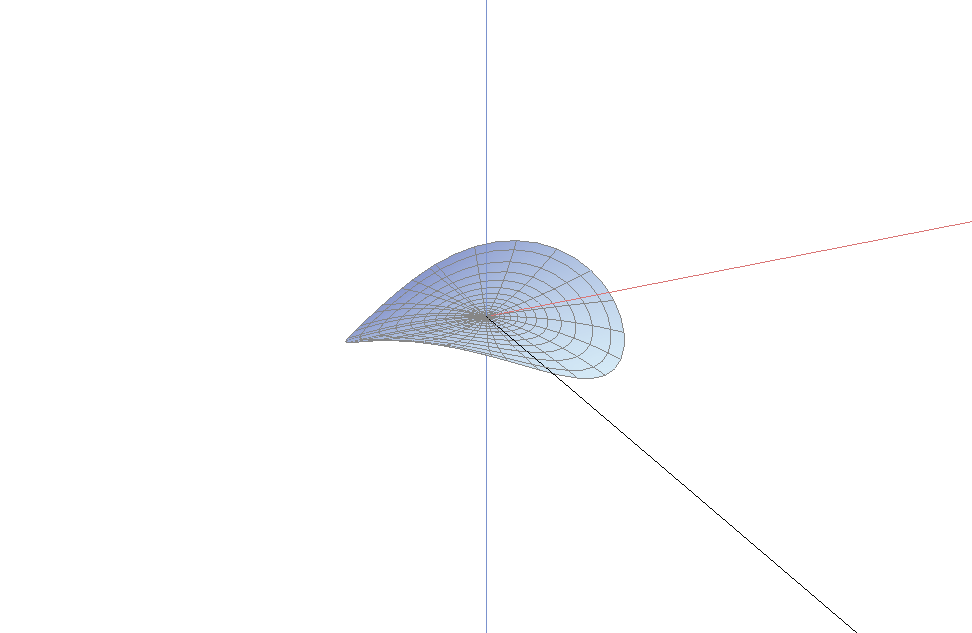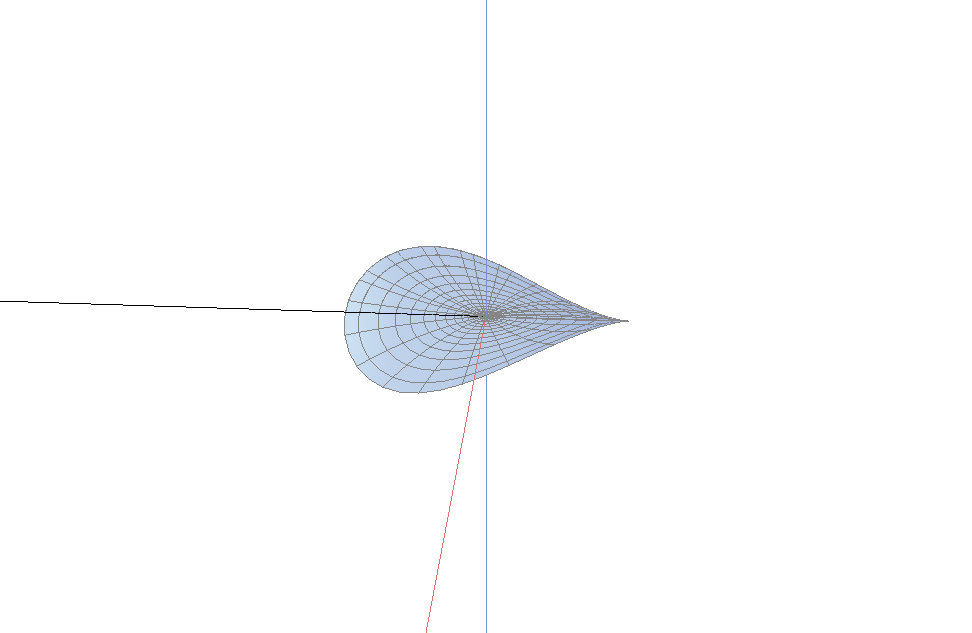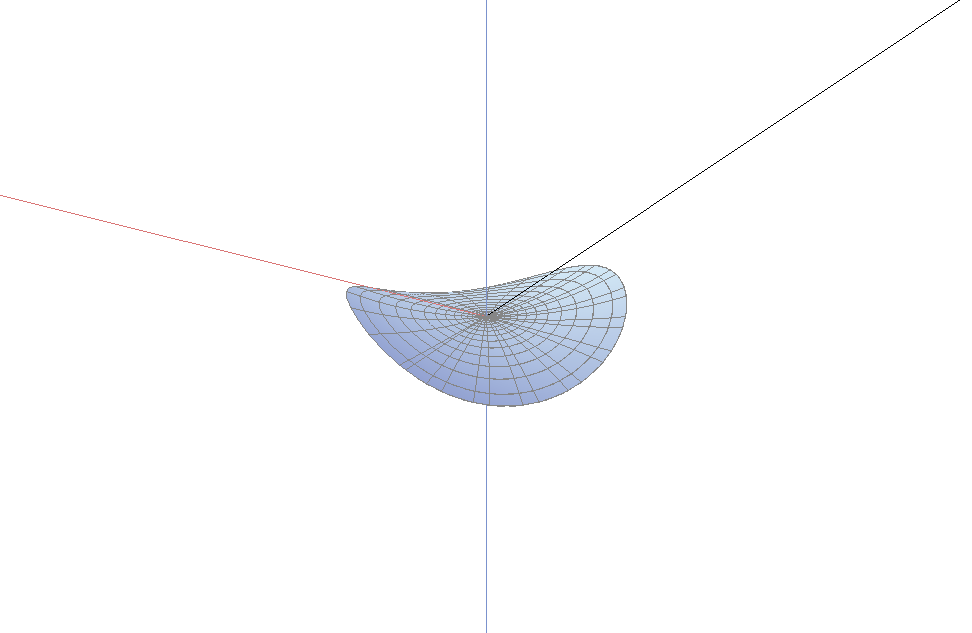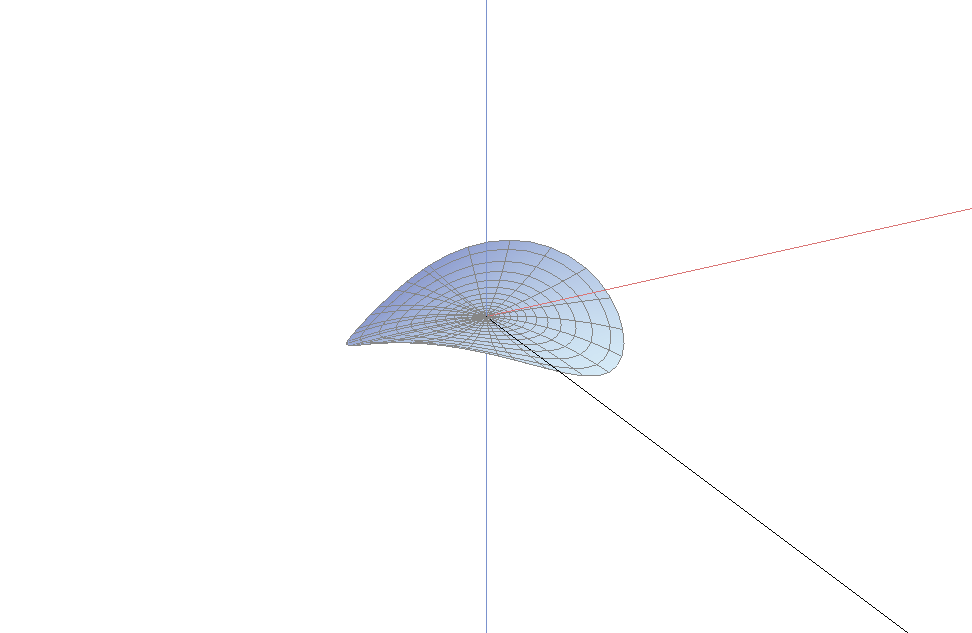
这些图形被两个整数完全刻画: 阶(order)以及指数(index). 分枝点可以分为内部分枝点和边界分枝点. 我们首先来看边界分枝点的图像
上面两个图中不容易看出的一个事实是: 单位法向量可以连续地延拓到分枝点(图像的中心). 这表明, 曲面的每片在中心附近都可以拉平成一个水平的曲面. 因此, 我们只需考虑分枝点附近的一个小邻域, 则从图像上看, 曲面变得更加的平坦. 下图是半径为$0.2$, 阶2指数1的一个分枝点, 从图中你可以看到曲面的法向量在原点附近趋于垂直方向.
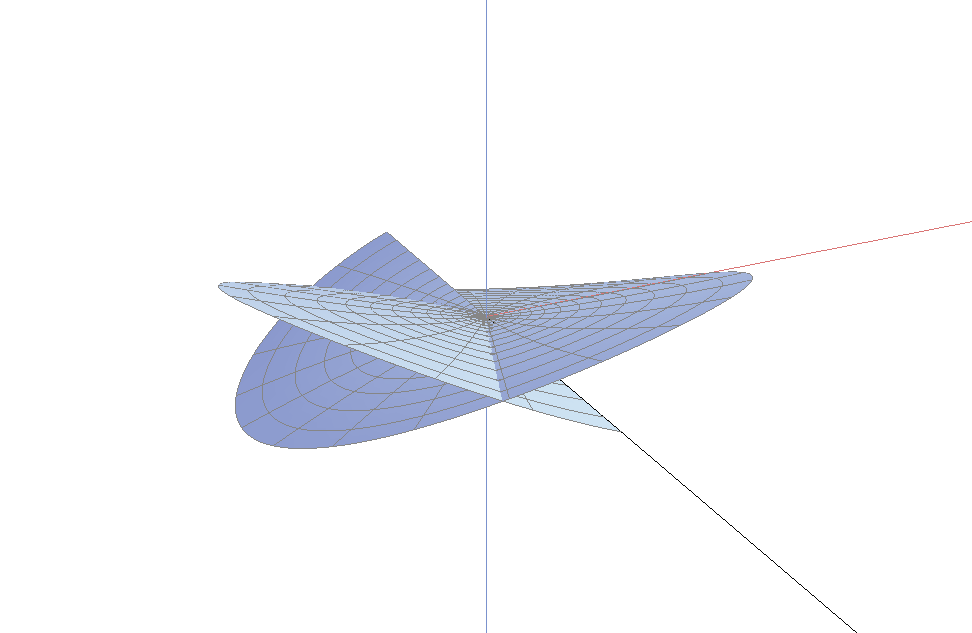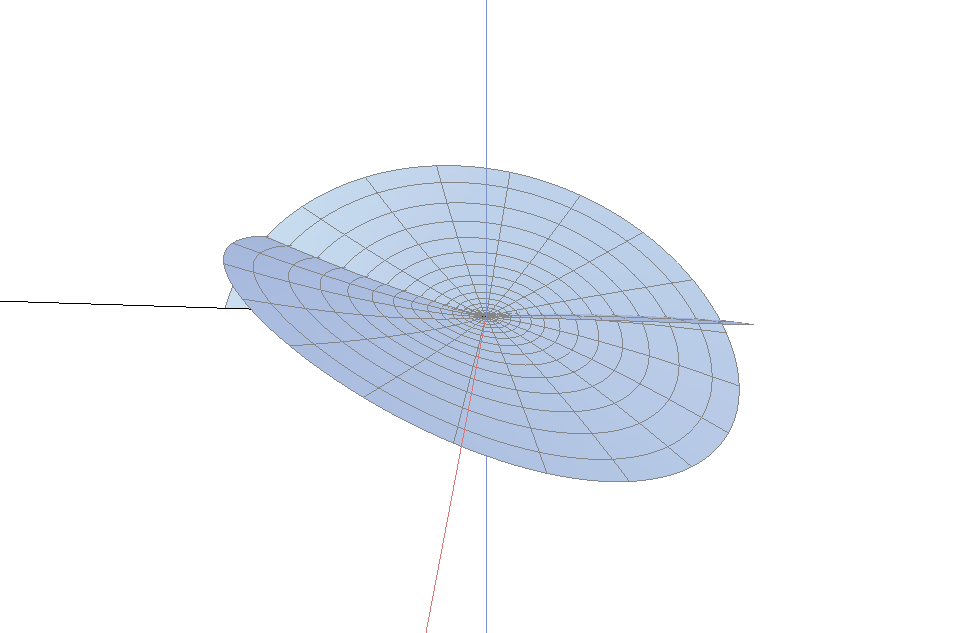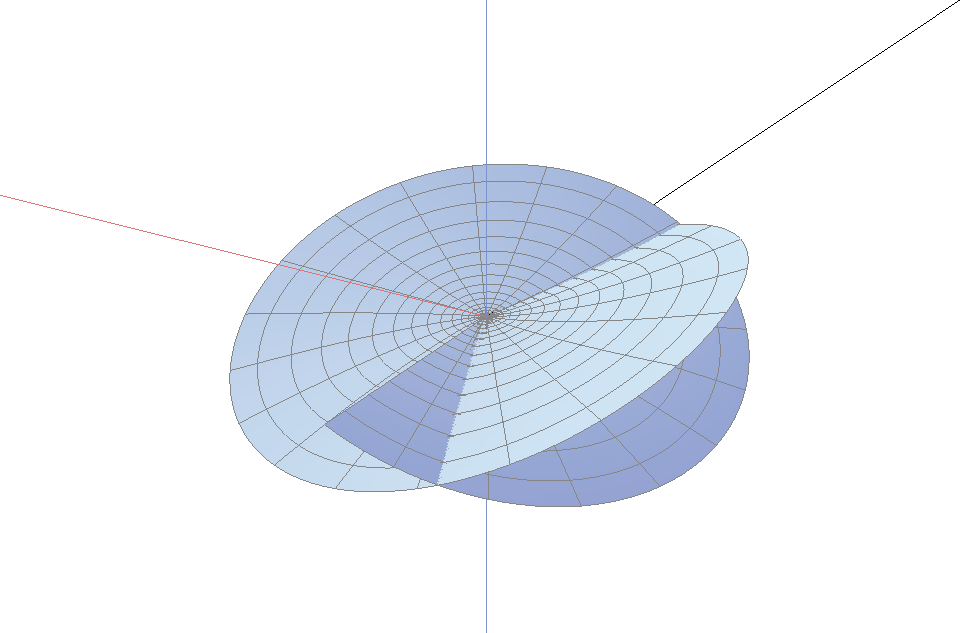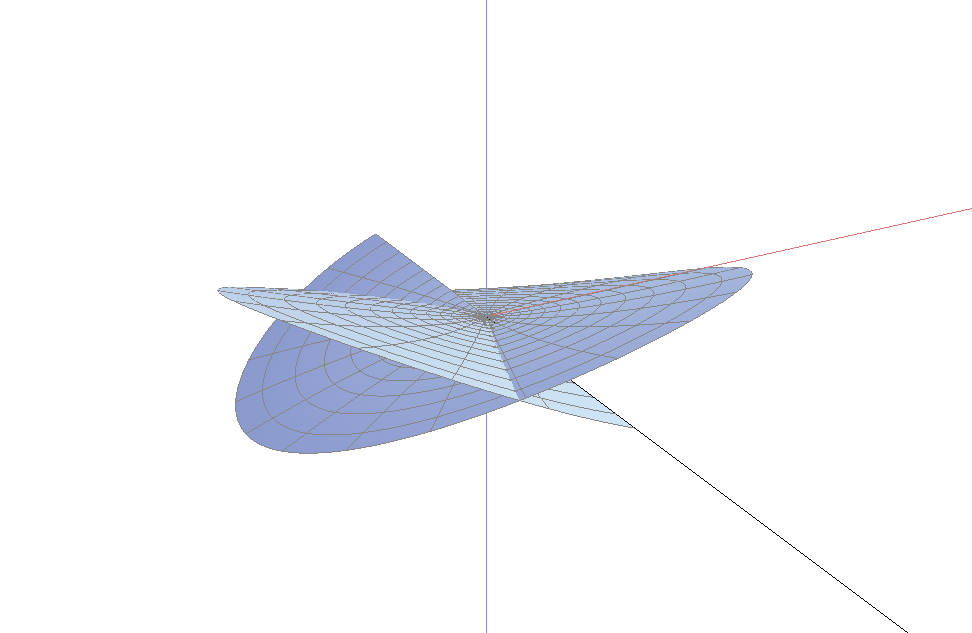
这些分枝点之所以称为边界分枝点, 是因为它们可能位于曲面的边界. 事实上, 图上的边界是一条直线(从图上你只看到了曲面的边界的一部分). 事实上, 图中也显示了$x$, $y$, $z$轴的一部分.
下图是分枝点为内点的情形, 本质上, 上面第一幅图是下图的一半.
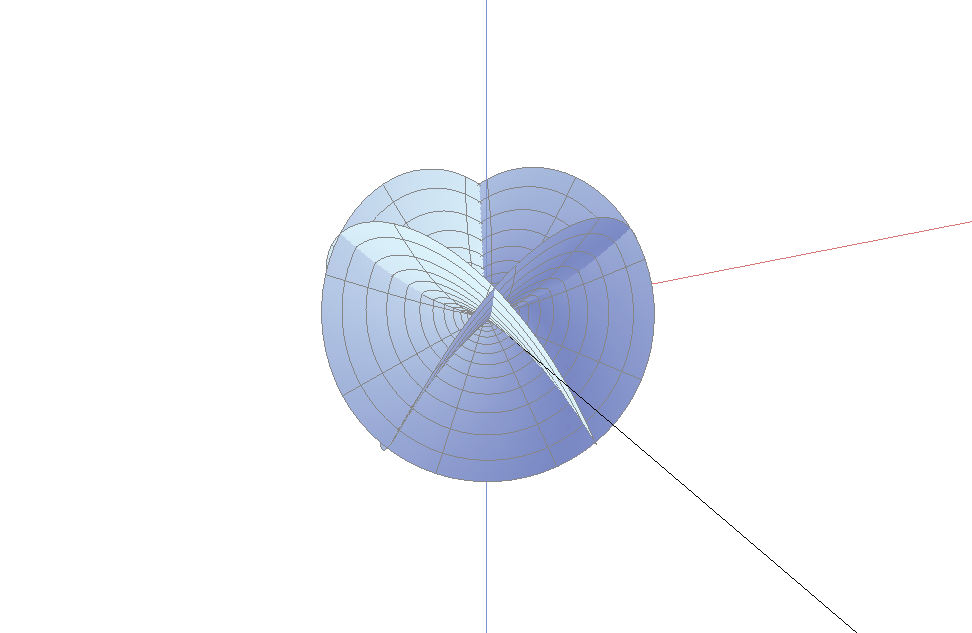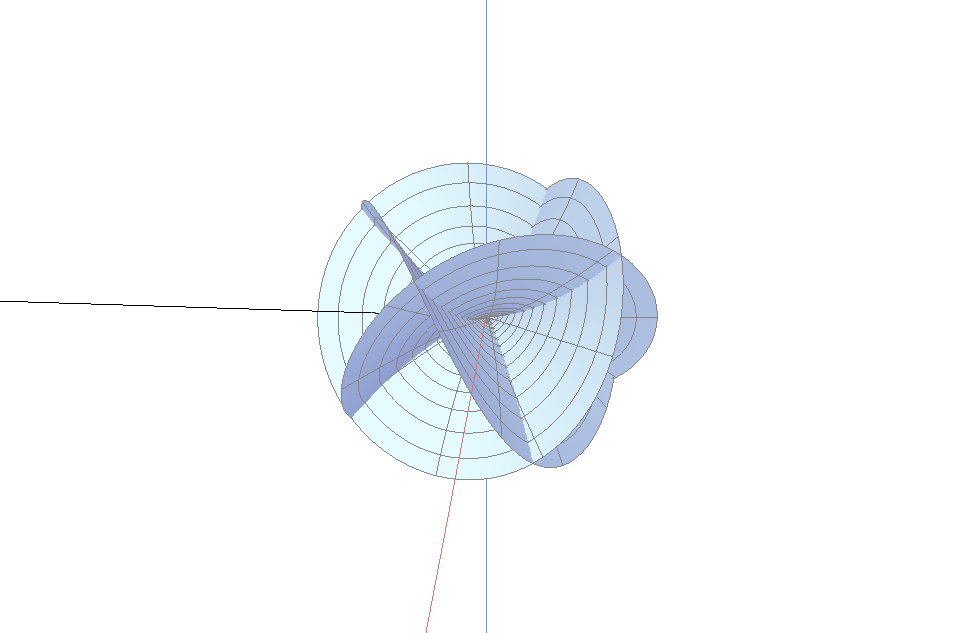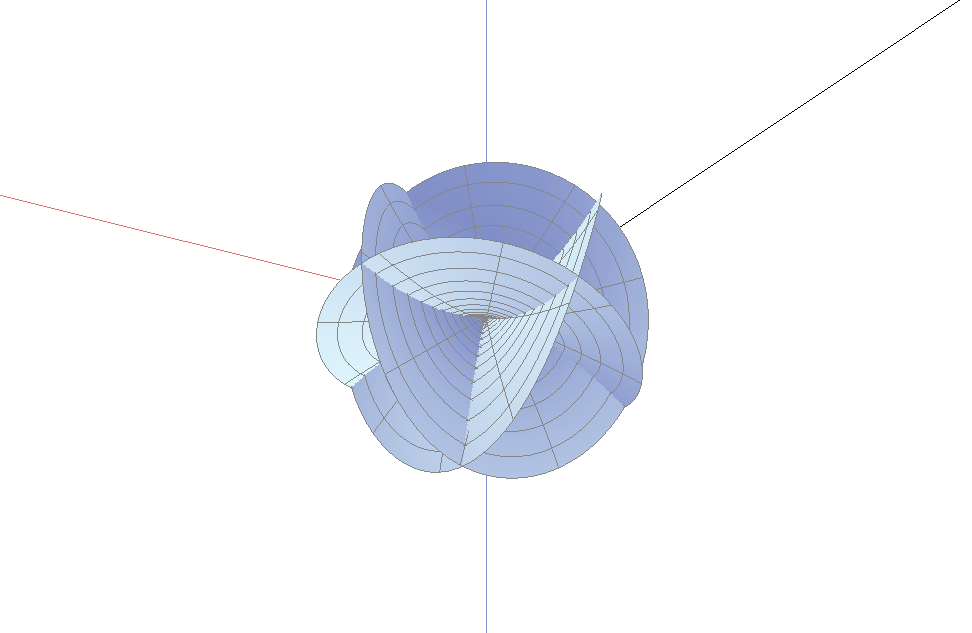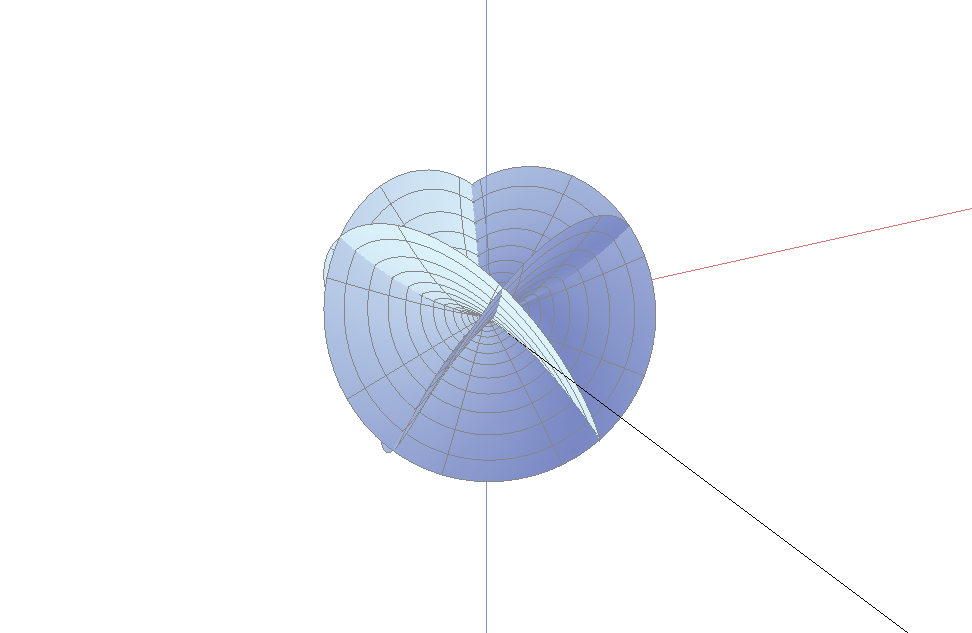
一个阶为$M$指数为$k$的分枝点的曲面绕了$M+1$次以及上下穿过$M+k+1$次. 当分枝点在边界时, 我们只看到该曲面的一半. 因此, 当曲面与边界单调地接触时, 边界分枝点的阶必为偶数; 当曲面与边界接触是两次绕回时, 边界分枝点的阶必为奇数. 因此, 阶为2时是最简单的情形. 指数为0将给出平面的一部分, 而指数为1是最简单的三维情形. 而阶为2, 指数为1作为内部分枝点, 将绕3次, 而且上下穿过4次; 而作为边界分枝点的话, 它将绕1.5次, 上下穿过2次. 一个4阶指数为2的边界分枝点, 将绕2.5次, 上下穿过3.5次. 这些正是上面各图所示的情况.
上面各个示例的图片中的曲面, 可以利用复变量$z$用如下简单公式刻画. 即, 如果曲面由三个参数给出$\{X(z),Y(z),Z(z)\}$, 那么它们满足
\begin{align*}
X+iY&=z^{M+1}/(M+1);\\
Z&=\mathrm{Re}[z^{M+k+1}/(M+k+1)]
\end{align*}
上述公式中, $\mathrm{Re}$表示一个复数的实部, 而第一个公式表明右端复数的实部和虚部分别为$X,Y$. 注意到如果$z$的极坐标为$(r,\theta)$, 那么
\begin{align*}
X&=\frac{1}{M+1}r^{M+1}\cos((M+1)\theta)\\
Y&=\frac{1}{M+1}r^{M+1}\sin((M_1)\theta),
\end{align*}
这个公式可以精确说明前面说的绕几圈. 事实上, 上面的图片我们显示的是的曲面定义在圆盘$|z|\leq 0.6$的这一部分.
对初学者一个有意思的问题是: 对曲面的一个阶为$M$指数为$k$的分枝点, 曲面的自交线有多少条?
任何一个分枝点必被类似地上述公式刻画. 但对$z$的高阶幂次, 可能有一些新的术语. 如果$M+1$正好整除$M+k+1$, 那么作为一次近似, 曲面将是周期重合的(如果你尝试解决上述问题, 那么你会注意到这个事实). 如果曲面可以分割成各个曲面片, 那么该曲面必须是由上述公式中高次幂给出的. 你可以看到下图中, 它表示边界分枝点的阶为2指数为3的情形. 因此$M+1=3$, $M+k+1=6$. 注意初看曲面像是扭曲的圆盘; 但是仔细观察, 通过曲面的坐标标记, 发现曲面事实上绕了1.5次, 它的后半次和第一个半次完全重合.
如果上述重合是精确的, 正如上图所示, 分枝点称为是伪分枝点. 但一定要注意曲面看起来几乎如此, 曲面的被很细的量分割成各个片(在计算机作图中甚至不可见), 这是因为它们是由$z$的高次幂的项决定的. 一个分枝点不是伪分枝点就称为真分枝点.
下图是一个曲面的更加复杂的分枝点