Definition 1. 假设$S_1,S_2$是两个曲面，$D_1\subset S_1$, $D_2\subset S_2$是两个开圆盘，即它们都同胚于标准欧氏平面上的单位圆盘。将$D_i$在$S_i$里的补集记作$S_i’$, 即$S_i’=S_i\setminus D_i$, $i=1,2$. 选取同胚映射$h:\partial D_1\to \partial D_2$, 则我们可以构造如下曲面$S_1\#S_2$：它是无交并集$S_1\sqcup S_2$商掉等价关系$\sim$, $x\sim y=h(x)$, 得到的商空间。即$S_1\#S_2=S_1\sqcup S_2/\sim$.
可以证明上述定义是良好的，即不依赖于圆盘$D_1, D_2$以及同胚映射$h$的选取。
2. 一个典型例子 明显地，按照定义任何曲面和球面的连通和就是它自己。两个环面的连通和就是亏格（洞的个数）为2的环面、继续和一个环面连通和则得到亏格为3的环面。如下图所示。
亏格为2的环面
亏格为3的环面
亏格为1的环面和亏格为2的环面的连通和
3. 一些曲面的连通和
回忆Mobius带是将一个长方形纸条的一对边反向粘贴而得到的（另一对边用虚线表示）。而射影平面是将一个正方形纸条或者单位圆盘的边界上对径点粘贴而得的曲面。
而Klein瓶可以视为将一个长方形纸条的一对对边同向粘贴、另一对对边反向粘贴而得到的。用图示表示如下：
Mobius带
射影平面
Klein瓶
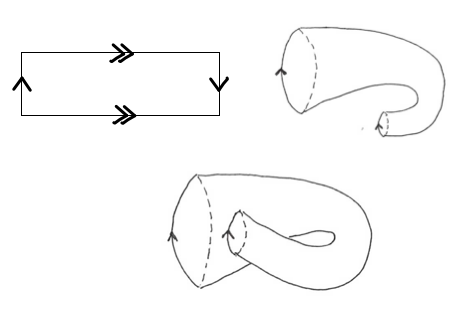
Example 1. 两个射影平面的连通和是Klein瓶。
Proof . 这个证明以及其中用到的图片都来自Connected sum of projective plane ≅ Klein bottle. 事实上，从图我们知道，Klein瓶是两个Mobius带粘贴而得。
而射影平面挖掉圆盘同胚于Mobius带。
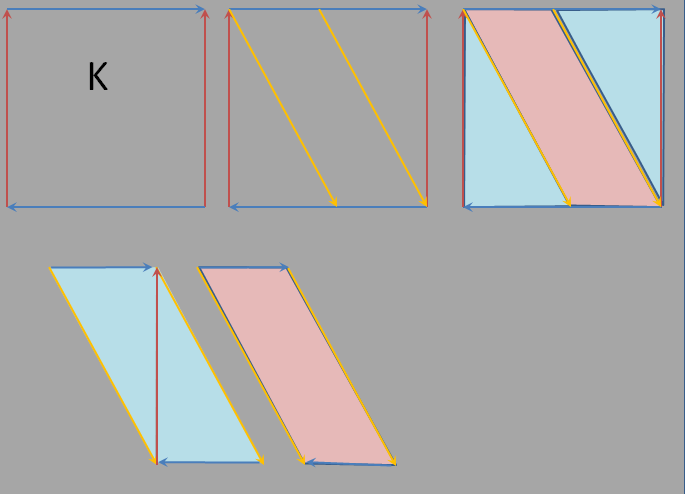
Klein瓶的分解
而射影平面挖掉圆盘同胚于Mobius带。
射影平面挖掉圆盘
Example 2. 三个射影平面的连通和是一个环面和一个射影平面的连通和。