为了方便理解Holder连续, 我这里举一个例子.
例子 1. 令$f(x)=|x|^{\alpha}$, $1>\alpha>0$, 则$\|f\|_{C^\alpha[-1,1]}=1$.
为了直观起见, 函数$f$的图形如下
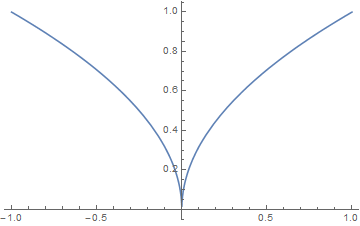
证明. 回忆Holder模的定义
\[
\|f\|_{C^\alpha[-1,1]}=\sup_{\substack{x\neq y\\x,y\in[-1,1]}}\frac{|f(x)-f(y)|}{|x-y|^\alpha}.
\]
为了计算其holder模, 注意到函数与定义域的对称性, 我们只需考虑如下两种情形
\[
\|f\|_{C^\alpha[-1,1]}=\sup_{\substack{x\neq y\\x,y\in[-1,1]}}\frac{|f(x)-f(y)|}{|x-y|^\alpha}.
\]
为了计算其holder模, 注意到函数与定义域的对称性, 我们只需考虑如下两种情形
- $0\leq x< y$, 此时可设$x=ky$, $k\in[0, 1)$ (请注意这个设法的良好性, 对任意满足条件的$x,y$一定存在$k$, 反过来对任意的$k$至少存在一对满足条件的$x,y$). 因此, 我们只需考虑函数$g(k,1)$在$[0,1)$上的极值, 其中
\[
g(x,y)\eqdef \frac{|f(x)-f(y)|}{|x-y|^\alpha}.
\]
容易求得$g([0,1))=(0,1]$.
事实上, 为了直观起见, 我给出此时该函数的图象如下
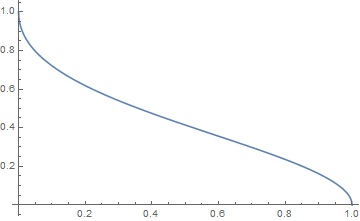
- $x< 0\leq y$且$|x|\leq|y|$, 此时可设$y=kx$, 且$k\in(-\infty,-1]$, 这里的设法的良好性同前理解. 求$g(1,k)$在$(-\infty,1]$的极值得到$g((-\infty,-1])=[0,1)$.
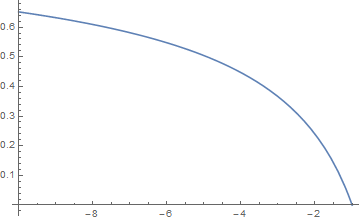
注记 1. 类似的讨论, 得出对$|x|^\alpha$, 它在$[-1,1]$上的$C^\beta$, $\beta\neq\alpha$模不存在.
