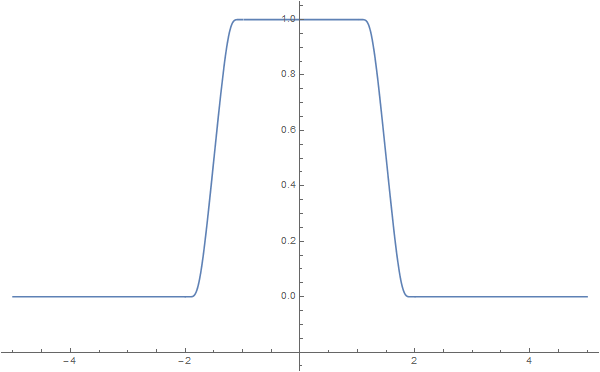
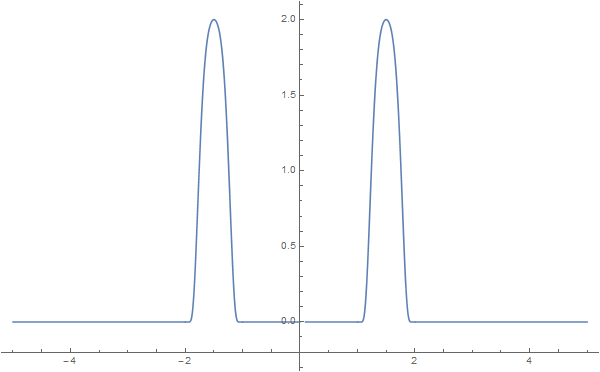
在实际应用过程中, 我们需要构造满足如下条件的截断函数:
$$
0\leq\phi\leq 1,\quad\phi|_{B_{1}}\equiv1,\quad \mathrm{supp}\phi\subset B_2,\quad\lvert \nabla\phi\rvert/\phi\leq 2.
$$
上诉截断函数可以具体的构造为:
\begin{align*}
f(t)&=\begin{cases}
e^{-1/t},&t>0\\
0,&t\leq0
\end{cases}\\
g(t)&=\frac{f(2-t)}{f(t-1)+f(2-t)}\\
\phi(t)&=g(|t|)
\end{align*}
可以验证
\begin{gather*}
\phi\in C^\infty,\quad
\phi|_{B_1}\equiv 1,\quad
\phi|_{B_2^c}\equiv 0,\quad
0\leq\phi\leq 1\\
\phi’/\phi=\begin{cases}
\frac{-(5-6|t|+2t^2)\exp\left(\frac{1}{2-3|t|+t^2}\right)\mathrm{Sign}(t)}{\left[(2-3|t|+t^2)\left(\exp\left(\frac{1}{1-|t|}\right)+\exp\left(\frac{1}{|t|-2}\right)\right)\right]^2},&1<|t|<2\\
0,&\text{otherwise}
\end{cases}
\end{gather*}
它们的图像分别如下