关于代数拓扑曲面分类定理:I

曲面分类定理的第一步是使用三角剖分，将曲面转化为简单多边形。Massey的书上列举了正方体的三角剖分转换为多边形的例子。这里，我们来看另一些例子。其基本想法是，通过对给定的剖分三角形重新编号$T_1,T_2,\ldots, T_n$, 使得$T_i$与$T_1,\ldots, T_{i-1}$至少有一条公共边, $i=2,3,\ldots, n$.

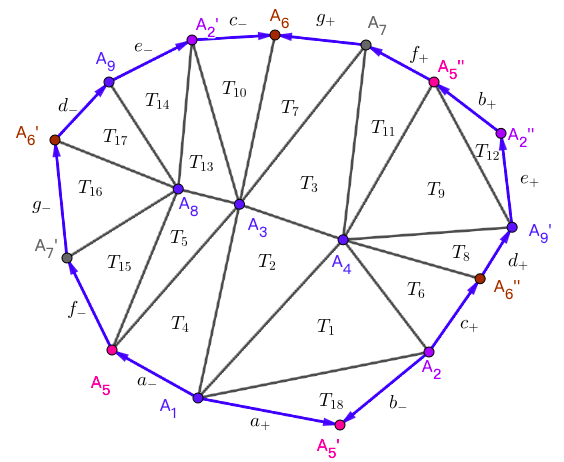
例子 1 ([1,Ex.~7.1, P.~21]). 三角剖分为

124 236 134 246
367 347 469 459
698 678 457 259
289 578 358 125
238 135

通过作图，得到剖分的曲面如图所示

最终得到的简化多边形为

即可等价描述为
$$
ab^{-1}cdebfgc^{-1}e^{-1}d^{-1}g^{-1}f^{-1}a^{-1}.
$$

例子 2 ([1,Ex.~7.2, P.~21]). 四面体的表面，其三角剖分为：

123 234 341 412

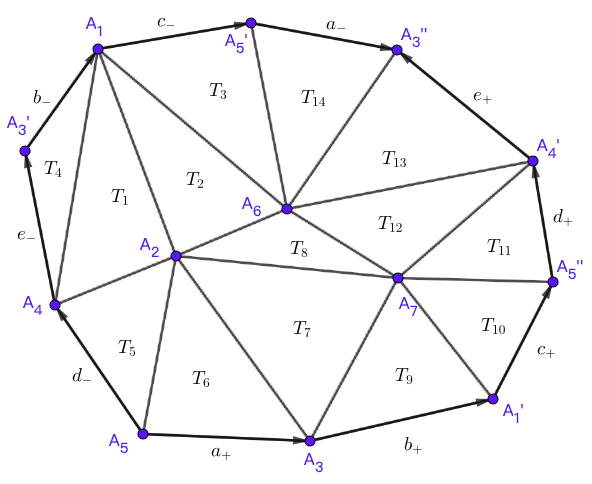
通过作图，最终得到的简化多边形如图所示：

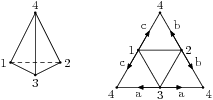
可等价描述为
$$
a^{-1}ab^{-1}bc^{-1}c.
$$

例子 3 ([1,Ex.~7.3, P.~21]). 射影平面, 其三角剖分为：

123 234 345 451 512
136 246 356 416 526

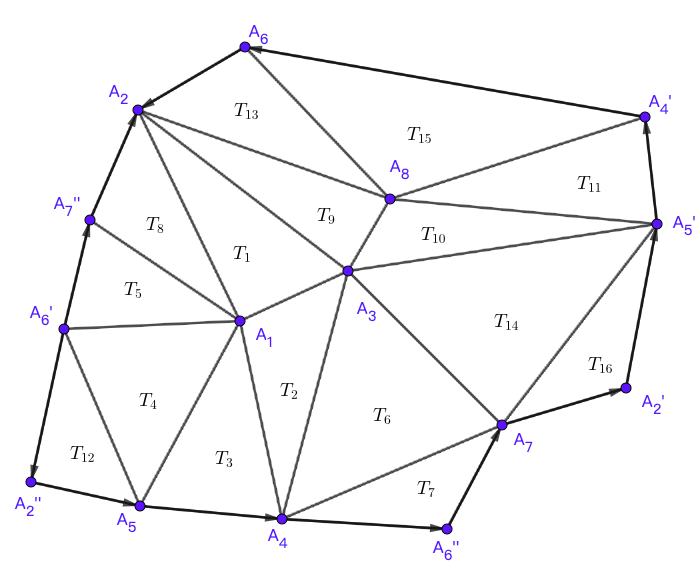
通过作图，

Massey_AlgebraicTopology_P21Ex7.3-triangulation.png

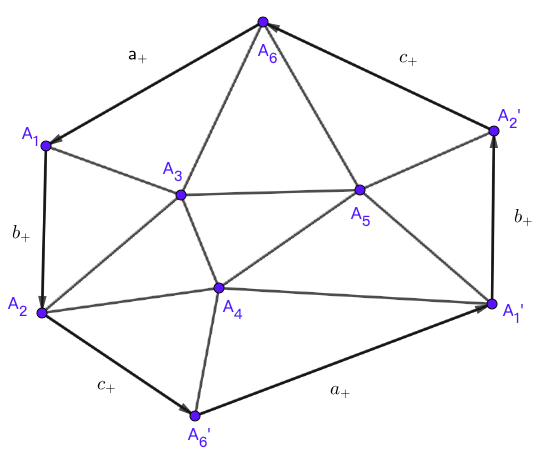
我们知道其简化多边形为

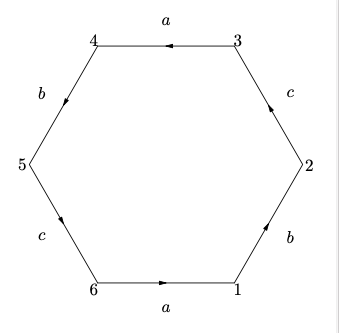
可等价描述为
$$
abcabc
$$

例子 4 ([1,Ex.~7.4, P.~21]). 三角剖分为：

124 235 346 457 561 672
713 134 245 356 467 571
126 237

作图得到

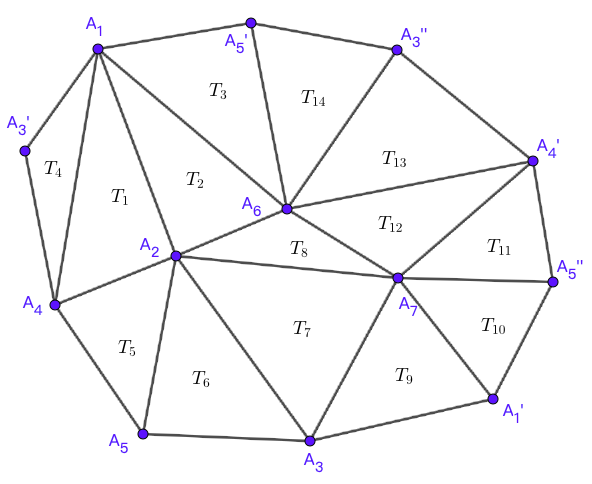
它的简化多边形为
$$abcdea^{-1}c^{-1}b^{-1}e^{-1}d^{-1}$$
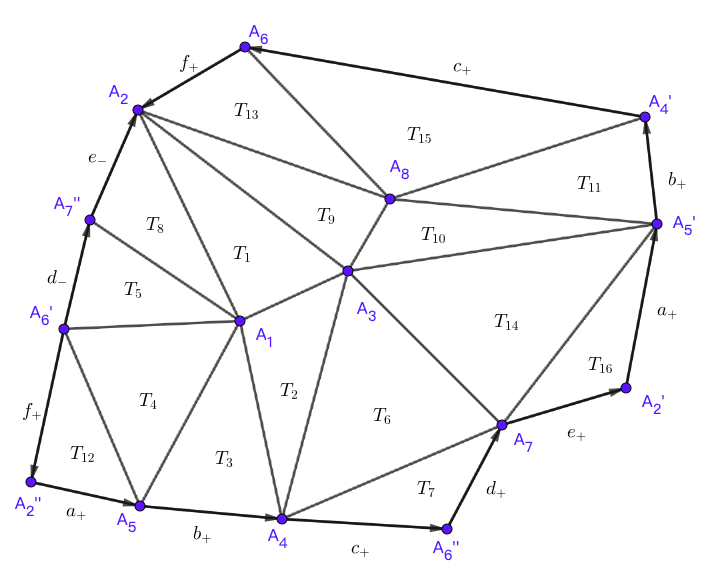
如图所示

例子 5 ([1,Ex.~7.5, P.~21]). 三角剖分为：

123 256 341 451
156 268 357 468
167 275 374 476
172 283 385 485

得到的简化多边形为

可等价表示为
$$
abcdeabcfe^{-1}d^{-1}f.
$$

参考文献

W. Massey, Algebraic topology: an introduction, Graduate Texts in Mathematics, Vol. 56, Springer-Verlag, New York-Heidelberg, 1977. 0---387. Reprint of the 1967 edition. MR0448331

发表评论 取消回复

发表评论取消回复