代数拓扑里面简化多边形的作图程序

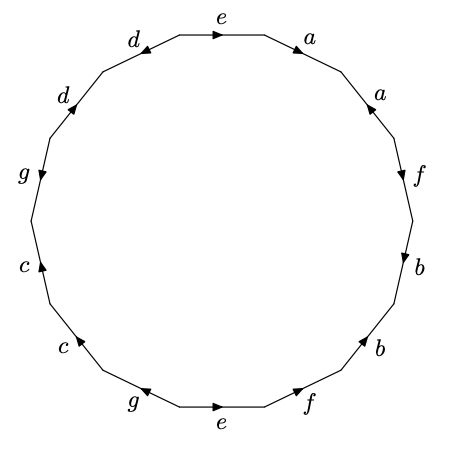
在代数拓扑里，我们将曲面视为将多边形的对应边粘贴而成的图形。当然一个重要的问题：
1. 如何将一个闭曲面三角剖分；
2. 如何从给定的三角剖分粘贴成多边形，使得三角剖分中公共的边作为多边形的内部的边、非公共边作为多边形真正的边。
一个操作过程可以参考[1,Chap.~1, Sec.~6].

这里，我们给出其中例子7.1中的三角剖分构造简化多边形的作图过程。代码如下：

\documentclass{minimal}
\usepackage{mpgraphics}
\begin{mpdefs}
  u:=10pt;
\end{mpdefs}
\begin{document}
\begin{mpdisplay}

input latexmp;
def ATdraw(text T)=
  save i_, n, s, edges;
  save poly; path poly;
  numeric n,i_; n=0;
  string s, edges[];
  s=str scantokens(T);
  show s;
  n:=length(s)/2;
  for i_=0 upto n-1:
    edges[i_+1]=substring(2i_,2i_+2) of s;
    show edges[i_+1];
  endfor;
  poly = for i=0 upto n-1: 80 down rotated (360/n*i-180/n) -- endfor cycle;
  string dr,lab;
  for i=1 upto n:
    dr := substring(length(edges[i])-1,length(edges[i])) of edges[i];
    lab := substring(0,length(edges[i])-1) of edges[i];
    show dr;
    show lab;
    if dr="1":
      drawarrow subpath(i-1,i-1/2) of poly;
      draw subpath(i-1/2,i) of poly;
    else:
      drawarrow subpath(i,i-1/2) of poly);
      draw subpath(i-1/2,i-1) of poly;
    fi;
    label(textext( "$" & lab & "$" ), 85 down rotated (360/n*(i-1)));
  endfor;
enddef;
ATdraw("e1 f1 b1 b0 f0 a1 a0 e0 d1 d0 g1 c0 c0 g0");

\end{mpdisplay}
\end{document}

其中，拉丁字母表示的是边，而拉丁字母后面的0或者1表示边的方向是顺时针或逆时针。

使用`xelatex -shell-escape

参考文献

W. Massey, Algebraic topology: an introduction, Graduate Texts in Mathematics, Vol. 56, Springer-Verlag, New York-Heidelberg, 1977. 0---387. Reprint of the 1967 edition. MR0448331

发表评论 取消回复

发表评论取消回复