$$ 则, 当下列条件之一满足时, 我们有, 对$\Omega$在$x_0$处的外法向量$\nu$, $$ 那么这样的$v$是否存在呢? 注意, 弱极大值原理表明(椭圆方程的解的)边界值在一定条件下可控制内部的值, 因此我们希望$u+v$在$\pt A$的值$\geq0$, 且$L(u+v)\geq0$, $\forall x\in A$. 回忆在证明弱极值原理时, 我们作小扰动的辅助函数是$-\eps e^{\lambda x_1^2}$, 当$\lambda$充分大时, 它在$L$的作用下是一个正项. 为了便于计算$\frac{\pt v}{\pt\nu}$的值. 我们这里改为尝试考察(注意我们假设了$(u+v)(x_0)=0$) $$ 注意到$\pt A=(\bar A\cap\pt B)\cup(\pt A\cap B)$, 我们自然分成两部分来考察. 在$\bar A\cap\pt B$上, 我们知道$u(x)\geq u(x_0)$, $v(x)=-u(x_0)$, 可见此时成立 $$ 至于$u(x_0)=0$. 考察$\tilde L=L+c^-$, 此时有 $$
$$
L=-a^{ij}(x)D_{ij}+b^i(x)D_i+c(x),
$$
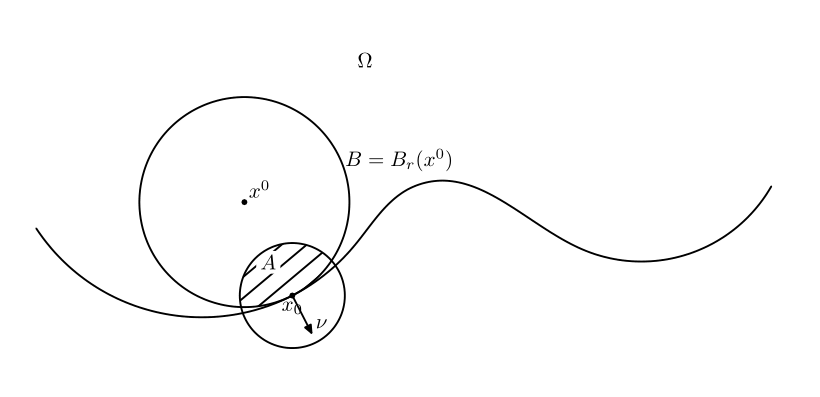
是$\Omega$上的一致椭圆算子($a^{ij}\xi_i\xi_j\geq\theta|\xi|^2$), $a^{ij}=a^{ji}$, $b^i$, $c$在$\bar\Omega$上连续. 假设$u\in C^2(\Omega)\cap C(\bar\Omega)$且$Lu\geq0$在$\Omega$中成立. 若存在半径为$r$的开球$B\subset\Omega$, 以及一点$x_0\in\pt B\cap\pt\Omega$, 使得
\frac{\pt u(x_0)}{\pt\nu}<0.
$$
$$
\frac{\pt u(x_0)}{\pt\nu}\leq0.
$$
为了证明严格不等式成立, 我们需要构造一个函数$v$, 使得它在$x_0$的一个邻域$A\subset\Omega$内有定义, $u+v$在$x_0$处取得$A$中取得极小, 特别, 由于求导与常数无关, 经过适当平移$v$, 可要求$(u+v)(x)\geq(u+v)(x_0)=0$, 这样我们将有
$$
0\geq\frac{\pt(u+v)(x_0)}{\pt\nu}=\frac{\pt u(x_0)}{\pt\nu}+\frac{\pt v(x_0)}{\pt\nu},
$$
因此我们只需要求$$\frac{\pt v(x_0)}{\pt\nu}>0$$即可.
v=\eps e^{\lambda r^2}-\eps e^{\lambda |x-x^0|^2}-u(x_0),
$$
其中$x^0$是$B$的球心.
注意到
$$
\frac{\pt v(x_0)}{\pt\nu}=-2\lambda r\eps e^{\lambda|x_0-x^0|^2}<0.
$$
这样, 看起来我们应该考虑
$$
v=\eps e^{-\lambda r^2}-\eps e^{-\lambda |x-x^0|^2}-u(x_0),
$$
此时便有
$$
\frac{\pt v(x_0)}{\pt\nu}=2\lambda r\eps e^{-\lambda r^2}>0.
$$
而这一改变不会改变$Lv$中关于$\lambda$的最高次项的符号. 事实上, 若令$c_0=\eps e^{-\lambda r^2}-u(x_0)$, 即$v=-\eps e^{-\lambda |x-x^0|^2}+c_0$, 则:
\begin{align*}
L(v)&=-\eps\left(-a^{ij}D_{ij}+b^iD_i\right)e^{-\lambda |x-x^0|^2}+cv\\
&=\eps e^{-\lambda |x-x^0|^2}\Bigg\{
4 \lambda^2a^{ij}(x_i-x^0_i)(x_j-x_j^0)\\
&\qquad\qquad\qquad\qquad-2\lambda\left(\sum_ia^{ii}-b^i(x_i-x_i^0)\right)
\Bigg\}+cv\\
&\geq\eps e^{-\lambda |x-x^0|^2}\Bigg\{
4 \lambda^2\theta\|x-x^0\|^2\\
&\qquad\qquad\qquad\qquad-2\lambda\left(\sum_ia^{ii}-b^i(x_i-x_i^0)\right)
\Bigg\}+cv\\
&\geq\eps e^{-\lambda|x-x^0|^2}\Bigg\{
4\theta\lambda^2\|x-x^0\|^2-2\lambda\left(\sum_ia^{ii}-r\|b\|\right)-c
\Bigg\}+cc_0\\
&\geq\eps e^{-\lambda|x-x^0|^2}\Bigg\{
4\theta\lambda^2\|x-x^0\|^2-2\lambda\left(\sum_ia^{ii}-r\|b\|\right)-c
\Bigg\}-cu(x_0)\\
\end{align*}
由此可见, 当$c\geq0$且$u(x_0)\leq0$时或者$c\equiv0$时, 若我们令$A=B\cap B_{r/2}(x_0)$且$\lambda$充分大时, 有
$$
L(v)\geq-cu(x_0)\geq0,\quad\forall x\in A.
$$
由此, 对任意的$\eps>0$, 都存在$\lambda>0$($\lambda$独立于$\eps$), 使得
$$
L(u+v)\geq L(v)\geq0,\quad\forall x\in A.
$$
于是, 由弱极大值原理, 有
$$
\min_{\bar A}(u+v)=\min_{\pt A}(-(u+v)^-).
$$
可见, 我们只需证明在$\pt A$上有$u+v\geq0$, 则$u+v\geq0$在$A$中成立.
u+v\geq0.
$$
在$\pt A\cap B\subset\pt A\cap \bar B$上, 有
$$\begin{align}
u(x)&>u(x_0),\\
v(x)&=\eps e^{\lambda r^2}-\eps e^{\lambda |x-x^0|^2}-u(x_0)\notag\\
&\geq \eps\left(e^{-\lambda r^2}-e^{-\lambda r^2/4}\right)-u(x_0),
\end{align}$$
可见此时我们可取$\eps$充分小, 使得,
$$
u+v>0.
$$
这样, 我们就完成了定理在$c\geq0$且$u(x_0)\leq0$情形的证明.
\tilde a^{ij}=a^{ij},\quad \tilde b_i=b_i,\quad \tilde c=c+c^-=c^+\geq0,
$$
且
$$
\tilde L u=Lu+c^-u\geq Lu\geq0,
$$
这是因为, 由假设$u(x)> u(x_0)=0$在$\Omega$中成立. 于是, 我们只需对$\tilde L$应用前面的结果即可.
最后, 我们将以一个注记来结束Hopf引理的笔记.